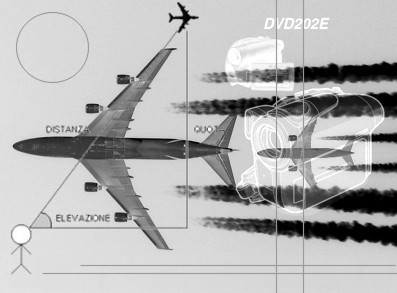
E' un classico imbattersi nella fatidica domanda: "Ma su quali basi puoi affermare che quel particolare velivolo si trovi ad una quota certa e non supposta?". Tale questione ha l'evidente scopo di smontare alle fondamenta il presupposto che i tankers chimici siano veramente tali e che, soprattutto, stiano spruzzando sostanze chimiche, non essendovi le condizioni per lo sviluppo di contrails. E' infatti vero che, se non si riesce a dimostrare la quota di volo di una aviocisterna, non si può nemmeno affermare inconfutabilmente che essa stia irrorando sostanze chimiche e che quelle scie al suo seguito non siano, invece, semplici scie di condensazione. Per i più distratti riassumo il principio fisico secondo il quale le scie di condensa si possono verificare solo a derminate condizioni di quota (oltre 8.000 metri), umidità (oltre il 72%) e temperatura (41° Celsius sotto lo zero). Ecco quindi che la trigonometria ci fornisce il mezzo principe per smontare la tipica malfidata opposizione del debunker: "Non puoi essere certo della quota".
Calcolo trigonometrico della quota
Per stimare la quota di un aereo è necessario conoscere la distanza tra l'aereo medesimo e l'osservatore (in questo caso la videocamera) e l'elevazione (o altezza), cioè la distanza angolare dell'aereo dall'orizzonte.
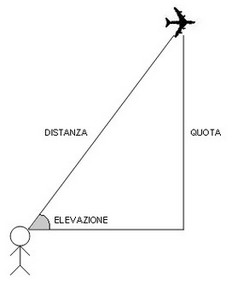La formula per trovare la quota Q conoscendo la distanza D e l'elevazione E è la seguente:Q = D * sin(E)
La condizione migliore è che l'aereo sia quasi sulla verticale dell'osservatore. In questo caso la quota sarà quasi uguale alla distanza, quindi basterà calcolare solo la distanza senza applicare la suddetta formula. Se l'aereo non risulta sulla verticale, si dovrà in qualche modo stimare l'elevazione.
Per calcolare la distanza, è necessario che:
1) siano conosciute la lunghezza focale dell'obiettivo e le dimensioni del CCD (diagonale oppure larghezza e altezza) della videocamera;
2) la videocamera possa bloccare lo zoom a un valore predefinito e conosciuto, e nel video sia presente un'inquadratura dell'aereo con quello zoom.
Se la videocamera memorizza il valore di zoom o di lunghezza focale durante la ripresa, il punto 2 non è necessario.
Per conoscere la lunghezza focale e le dimensioni del CCD, consultare il manuale della videocamera (di solito alla voce "Caratteristiche tecniche").
La lunghezza focale è espressa da due valori in millimetri (per esempio: 5 - 50 mm), e di solito è scritta sull'obiettivo stesso. Ci servirà soltanto il valore più piccolo.
Le dimensioni del CCD possono essere espresse in vari modi. Di solito è presente un valore espresso come frazione di un pollice (per esempio 1/4") e la lunghezza della diagonale in millimetri. Se è presente solo il valore in pollici, cercare su internet il valore corrispondente della diagonale, o anche le dimensioni di larghezza e altezza, se presenti. Conoscendo la diagonale, calcoliamo la larghezza del CCD con la seguente formula:
Larghezza = 4/5 * diagonale
A questo punto si può procedere con la misurazione vera e propria.
Tra i fotogrammi ripresi con il valore di zoom conosciuto, individuare quello dove l'aereo risulta più nitido. Esportare il fotogramma per aprirlo con un programma di grafica e misurare la lunghezza dell'aereo in pixel.
La distanza D dell'aereo si calcola con la seguente formula:
D = ( LA * LVP * F * Z ) / ( LC * LAP )
LA = lunghezza reale dell'aereo
LVP = larghezza del video in pixel
F = lunghezza focale minima
Z = zoom
LC = larghezza del CCD
LAP = lunghezza dell'aereo in pixel
ESEMPIO
Si suppone che l'aereo abbia una lunghezza approssimativa di 50 m.
Dati della videocamera:
Lunghezza focale: 3,0 - 36 mm
Diagonale CCD: 3,27 mm
Larghezza del CCD:
larghezza = 4/5 * 3,27 = 2,62 mm
Calcolo della distanza:
D = ( 50 * 1024 * 3 * 12 ) / ( 2,62 * 110 ) = 6.396 m
Poiché l'aereo si trovava praticamente al di sopra dell'osservatore, possiamo affermare che la quota dell'aereo era circa 6.400 metri.
Affinchè il calcolo sia inequivocabile, consiglio di prendere come riferimento un aereo del quale si conosca l'effettiva lunghezza.
In conclusione...
Se le immagini dei filmati, ad esempio, sono larghe 740 pixel. La formula, quindi, sarà:
D= (50*740*3*12) / (2.62*110) = 4621,791 metri
Calcolo della quota con metodo empirico
Vi è un altro modo "empirico" (senza perciò dover usare strumentazione adeguata) per valutare la distanza dall'osservatore all'oggetto: le sue dimensioni sulla verticale ad occhio nudo. Essendo note le dimensioni reali del velivolo (apertura alare o lunghezza della carlinga), si fa presto a calcolarne la quota, raffrontandola con le dimensioni risultanti ad occhio nudo.
Si prenda come riferimento un edificio di 40 metri (l'apertura alare di un KC-135) di larghezza e se ne misurino le dimensioni apparenti ad occhio nudo ed alla distanza di 3.000 metri.
Si rapporti quindi tale misurazione con le dimensioni risultanti, sempre ad occhio nudo, durante l'avvistamento sulla propria verticale, di un velivolo dalle caratteristiche prese come riferimento. Se ne dedurrà la distanza.
Esempio:
Se un edificio, largo 40 metri, misura 8 millimetri alla distanza di 2.000 metri, parimenti, un KC-135 che misurerà 4 millimetri, sarà certamente alla quota di 4.000 metri.
Metto a disposizione di quanti ne volessero fare uso, un file in formato html, che si potrà usare in locale (sul proprio PC), quindi senza dover accedere al sito:
... grazie al quale ho potuto estrapolare quanto necessitava.
Per mezzo di tale script, elaborato partendo dal codice html/java della pagina suddetta, chiunque avrà la necessità di calcolare quota e velocità dei velivoli "irroranti", potrà velocemente ottenere il risultato, semplicemente inserendo i dati nelle tabelle predisposte. Lo script può essere scaricato da QUI.
Per usare l'"Altitude calculator" del sito americano proposto, occorre compilare il form con quattro valori, tre dei quali (larghezza in pixel dell'immagine, lunghezza in pixel e lunghezza reale dell'aereo) sono facilmente calcolabili.
Per calcolare l'angolo di campo orizzontale (angle of view), bisogna utilizzare il form "35mm equivalent focal length" presente più in basso nella stessa pagina.
Inserire la lunghezza focale (focale minima * zoom) nel campo "Film Focal Length" e la larghezza del CCD nel campo "Film horizontal". Gli altri campi non ci interessano.
Cliccando sul pulsante Calculate, si ottiene l'angolo di campo orizzontale nel campo "FoV horizontal".
Nel nostro esempio, inseriamo i campi:
Film Focal Length: 36
Film horizontal: 2.62
Il risultato è
FoV horizontal: 4.17
Inserendo i dati nel primo form:
Total pixel width of full image: 1024
Angle of view (degrees): 4.17
Pixel span of aircraft: 110
Actual span (feet or meters): 50
Il risultato è
Altitude (feet or meters): 6386
Solo 10 metri di differenza rispetto al risultato della mia formula.
Si può quindi scegliere indifferentemente l'uno o l'altro metodo.
La distanza D dell'aereo si calcola con la seguente formula:
D = ( LA * LVP * F * Z ) / ( LC * LAP )
LA = lunghezza reale dell'aereo
LVP = larghezza del video in pixel
F = lunghezza focale minima
Z = zoom
LC = larghezza del CCD
LAP = lunghezza dell'aereo in pixel
ESEMPIO
Si suppone che l'aereo abbia una lunghezza approssimativa di 50 m.
Dati della videocamera:
Lunghezza focale: 3,0 - 36 mm
Diagonale CCD: 3,27 mm
Larghezza del CCD:
larghezza = 4/5 * 3,27 = 2,62 mm
Calcolo della distanza:
D = ( 50 * 1024 * 3 * 12 ) / ( 2,62 * 110 ) = 6.396 m
Poiché l'aereo si trovava praticamente al di sopra dell'osservatore, possiamo affermare che la quota dell'aereo era circa 6.400 metri.
Affinchè il calcolo sia inequivocabile, consiglio di prendere come riferimento un aereo del quale si conosca l'effettiva lunghezza.
In conclusione...
Se le immagini dei filmati, ad esempio, sono larghe 740 pixel. La formula, quindi, sarà:
D= (50*740*3*12) / (2.62*110) = 4621,791 metri
Calcolo della quota con metodo empirico
Vi è un altro modo "empirico" (senza perciò dover usare strumentazione adeguata) per valutare la distanza dall'osservatore all'oggetto: le sue dimensioni sulla verticale ad occhio nudo. Essendo note le dimensioni reali del velivolo (apertura alare o lunghezza della carlinga), si fa presto a calcolarne la quota, raffrontandola con le dimensioni risultanti ad occhio nudo.
Si prenda come riferimento un edificio di 40 metri (l'apertura alare di un KC-135) di larghezza e se ne misurino le dimensioni apparenti ad occhio nudo ed alla distanza di 3.000 metri.
Si rapporti quindi tale misurazione con le dimensioni risultanti, sempre ad occhio nudo, durante l'avvistamento sulla propria verticale, di un velivolo dalle caratteristiche prese come riferimento. Se ne dedurrà la distanza.
Esempio:
Se un edificio, largo 40 metri, misura 8 millimetri alla distanza di 2.000 metri, parimenti, un KC-135 che misurerà 4 millimetri, sarà certamente alla quota di 4.000 metri.
Metto a disposizione di quanti ne volessero fare uso, un file in formato html, che si potrà usare in locale (sul proprio PC), quindi senza dover accedere al sito:
... grazie al quale ho potuto estrapolare quanto necessitava.
Per mezzo di tale script, elaborato partendo dal codice html/java della pagina suddetta, chiunque avrà la necessità di calcolare quota e velocità dei velivoli "irroranti", potrà velocemente ottenere il risultato, semplicemente inserendo i dati nelle tabelle predisposte. Lo script può essere scaricato da QUI.
Per usare l'"Altitude calculator" del sito americano proposto, occorre compilare il form con quattro valori, tre dei quali (larghezza in pixel dell'immagine, lunghezza in pixel e lunghezza reale dell'aereo) sono facilmente calcolabili.
Per calcolare l'angolo di campo orizzontale (angle of view), bisogna utilizzare il form "35mm equivalent focal length" presente più in basso nella stessa pagina.
Inserire la lunghezza focale (focale minima * zoom) nel campo "Film Focal Length" e la larghezza del CCD nel campo "Film horizontal". Gli altri campi non ci interessano.
Cliccando sul pulsante Calculate, si ottiene l'angolo di campo orizzontale nel campo "FoV horizontal".
Nel nostro esempio, inseriamo i campi:
Film Focal Length: 36
Film horizontal: 2.62
Il risultato è
FoV horizontal: 4.17
Inserendo i dati nel primo form:
Total pixel width of full image: 1024
Angle of view (degrees): 4.17
Pixel span of aircraft: 110
Actual span (feet or meters): 50
Il risultato è
Altitude (feet or meters): 6386
Solo 10 metri di differenza rispetto al risultato della mia formula.
Si può quindi scegliere indifferentemente l'uno o l'altro metodo.
Ringraziamenti:
Desidero ringraziare Emilius per il suo indispensabile contributo.
Nessun commento:
Posta un commento
ATTENZIONE! I commenti sono sottoposti a moderazione prima della loro eventuale pubblicazione.
Nota. Solo i membri di questo blog possono postare un commento.